3481.阶乘的和

3481.阶乘的和

⭐️难度：简单（感觉较难）
⭐️类型：模拟

📖题目：题目链接

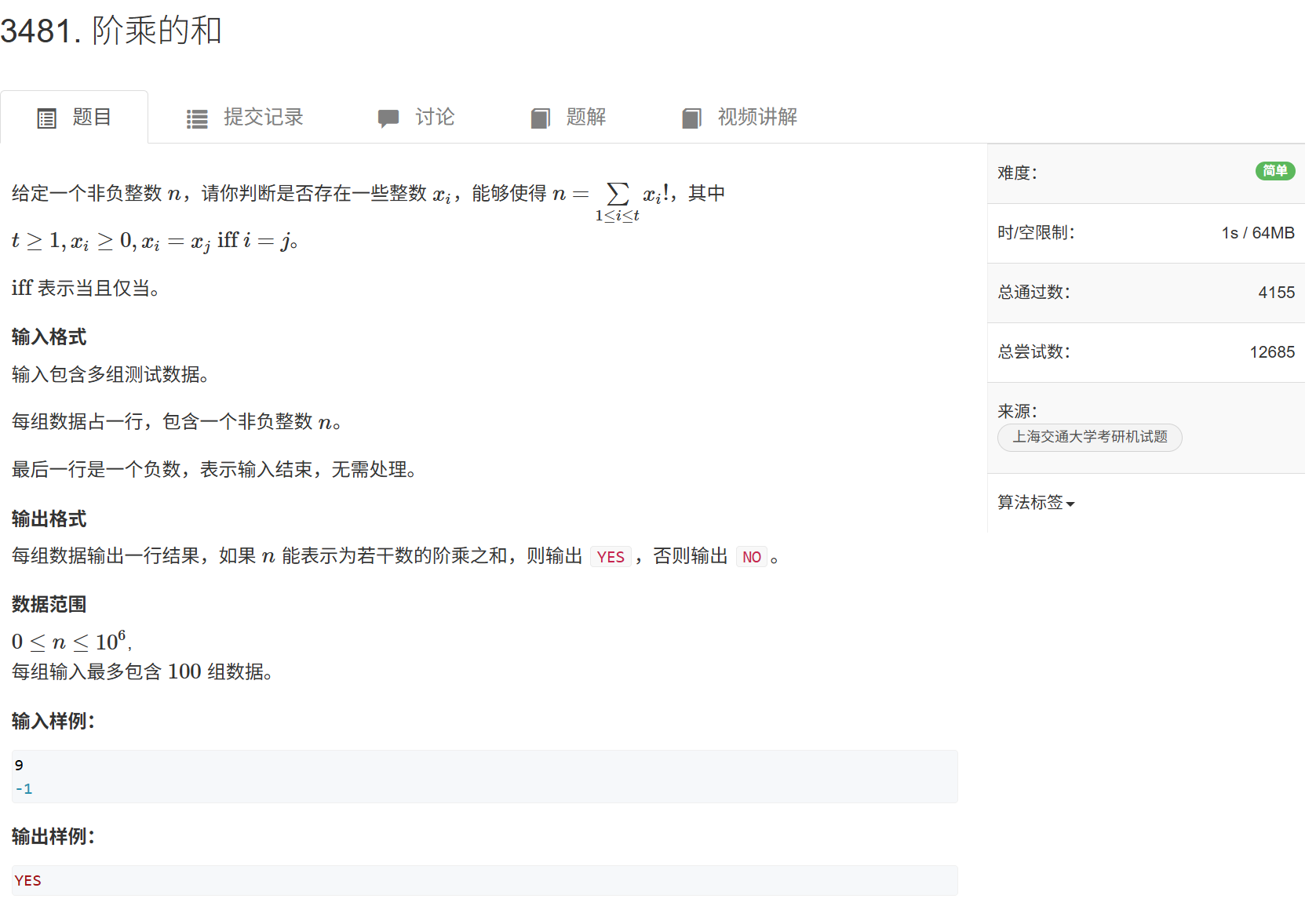
t≥1：至少有一项；
xi=xj iff i=j：说明 不允许重复使用同一数字。

🌟思路：
先计算小于1000000的阶乘，

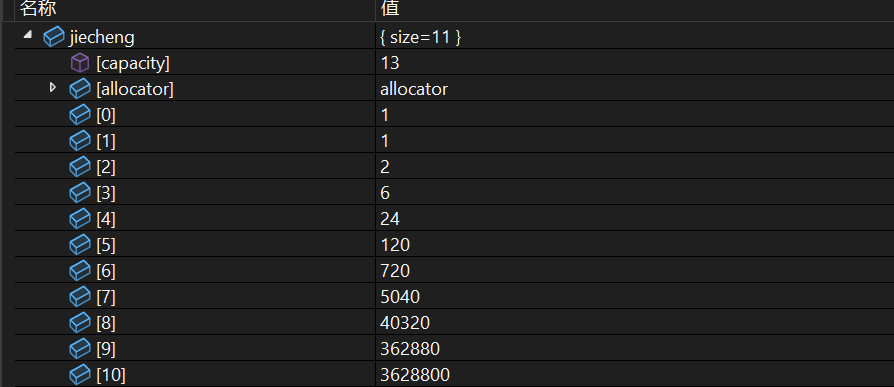
因为小于1000000的阶乘个数只有10个（0~9），非常有限，
所以考虑一个数能否由几个数的阶乘组成，我们可以先计算所有可能的阶乘之和，用空间换时间。

1️⃣那么，总共有几种可能呢？

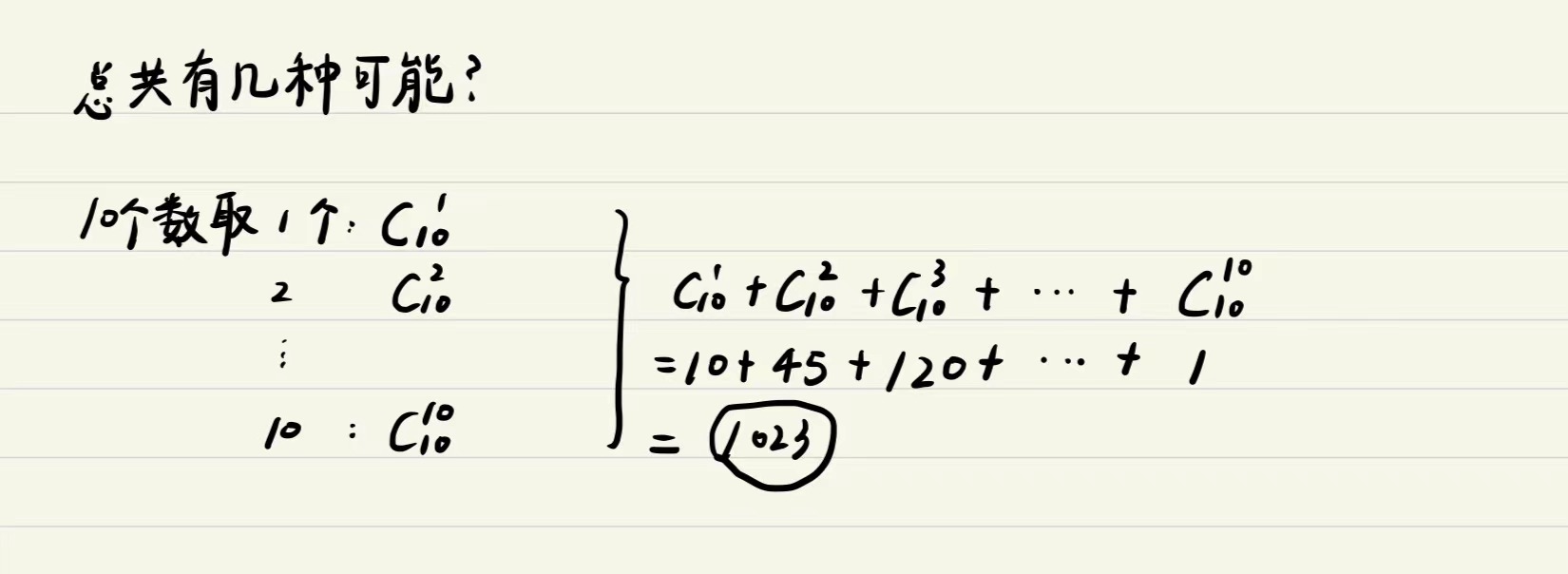
答：1023种可能。

2️⃣那么，怎么计算1023个阶乘之和呢？
1、先初始化一个set（作用是使阶乘之和不重复），初始数据是{0}（0的作用是计算1!,2!,3!..)；
2、从0!开始，set的每一个元素都加上0!，结束后set有2个数据，
再遍历到1!，set的每一个元素都加上1！，结束后set有4个数据… …；
3、循环结束后，就得到了1023个阶乘之和。
4、由于题目要求至少有一个数字，也就是阶乘之和不为0，最后再删除掉set中的0。

📚题解：
自己写：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>
#include<vector>  // vector不需要.h
#include<list>
#include<set>  // // 可以用 set 和 multiset
#include<unordered_set> // 可以用 unordered_set 和 unordered_multiset
using namespace std;
int main() {
    vector<int> jiecheng;
    int sum = 1;
    jiecheng.push_back(1);  // 0的阶乘为1，先push进数组
    for (int i = 1;i <= 9;i++) { // 计算阶乘小于1000000的数，10的阶乘已经超1000000
        sum = sum * i;
        jiecheng.push_back(sum);
    }
    // 计算1023个阶乘之和
    set<int> he; // 存阶乘之和
    he.insert(0); // 插入0，计算1!,2!,3!......
    for (int i = 0;i <= 9;i++) { // 遍历0~9，10个数字的阶乘
        set<int> temphe; // 暂存计算出来的阶乘之和，随后加到set里面
        set<int>::iterator it;
        for (it = he.begin();it != he.end();it++) {
            int num = *it + jiecheng[i];
            temphe.insert(num);
        }
        for (it = temphe.begin();it != temphe.end();it++) {
            he.insert(*it);
        }
    }
    // 按题目要求，删除0
    he.erase(0);
    int x;
    while (scanf("%d", &x) != EOF) {
        if (x < 0) {
            break;
        }
        if (he.find(x) != he.end()) {
            printf("YES\n");
        }
        else {
            printf("NO\n");
        }
    }
    return 0;
}

答案：

 #include <stdio.h>
 #include <set>
 #include <vector>
 using namespace std;
 int main() {
     vector<int> factorialArr;
     // 把0！放入数组
     factorialArr.push_back(1);
     int currentFactorial = 1;
     for (int i = 1; i <= 9; ++i) {
         currentFactorial = currentFactorial * i;
         factorialArr.push_back(currentFactorial);
     }
     set<int> allPossible; // 所有的阶乘和的可能性
     allPossible.insert(0);
     for (int i = 0; i <= 9; ++i) {
         set<int> tempSet;
         set<int>::iterator it;
         for (it = allPossible.begin(); it != allPossible.end(); ++it) {
             tempSet.insert(*it + factorialArr[i]);
         }
         for (it = tempSet.begin(); it != tempSet.end(); ++it) {
             allPossible.insert(*it);
         }
     }
     allPossible.erase(0);
     int n;
     while (scanf("%d", &n) != EOF) {
         if (n < 0) {
             break;
         }
         if (allPossible.count(n) == 0) {
             printf("NO\n");
         }
         else {
             printf("YES\n");
         }
     }
     return 0;
 }